1.1. Цифровой двойник представляет собой компьютерную модель метода конечных элементов (МКЭ) 1.1.1, предназначенную для расчета параметров напряженно-деформированного состояния 1.1.2 реального сооружения в зависимости от изменения нагрузок и воздействий, с учетом накопленной истории эксплуатации 1.1.3 сооружения и нелинейных 1.1.4 особенностей его работы (как применяется цифровой двойник рассмотрено в п. II).
1.2. Цифровой двойник учитывает фактическое 1.2.1 состояние сооружения, в частности, фактические свойства строительных материалов и грунтов основания, которые отличаются от проектных характеристик 1.2.2, установленных по нормам проектирования с запасом на естественную изменчивость свойств материалов (как мы подбираем фактические характеристики см. в п. III).
1.3. Цифровой двойник учитывает фактические нагрузки и воздействия 1.3.1, которые регистрируются в ходе мониторинга реального сооружения, вместо искусственно составленных наиболее неблагоприятных сочетаний нагрузок и воздействий, которые задаются при проектировании.
1.1.1. Метод конечных элементов (МКЭ) в настоящее время считается наиболее распространенным методом математического моделирования гидротехнических и других строительных сооружений. Он является основой большинства конструкторских и геотехнических расчетных программ и применяется для расчета напряженно-деформированного состояния, теплообмена и фильтрации [I.1, I.2, I.3, I.4, I.5].
Конечно-элементная модель представляет собой геометрическую модель сооружения, аппроксимированную сеткой из конечных элементов, которые имеют унифицированную форму (параллелепипед, призма, тетраэдр и т.п.) и соединяются между собой в узлах сетки.
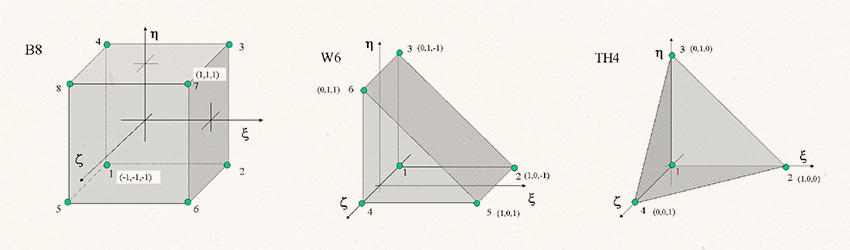
Размеры конечных элементов подбираются таким образом, чтобы аппроксимировать поля результатов (перемещения, деформации, напряжения). Поэтому размеры конечных элементов обычно изменяются в соответствии с характером изменения результатов.
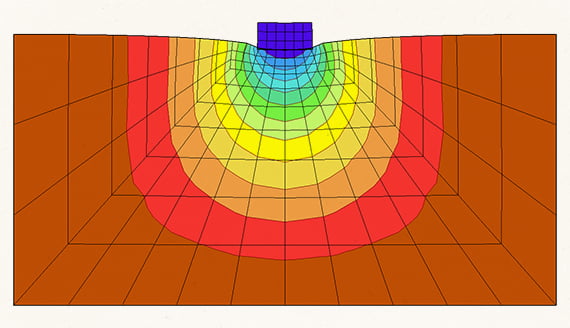
Чем больше конечных элементов, тем выше вычислительная сложность модели, поэтому общее количество конечных элементов должно быть оптимальным. Это важно для цифровых двойников, т.к. они предназначены для многократных расчетов напряженно-деформированного состояния сооружения по мере изменения нагрузок и воздействий (вплоть до сотен и тысяч расчетных этапов), что генерирует большой объем данных.
Цифровой двойник обычно создается в постановке «сооружение – основание», охватывая как само сооружение, так и представительный объем основания.
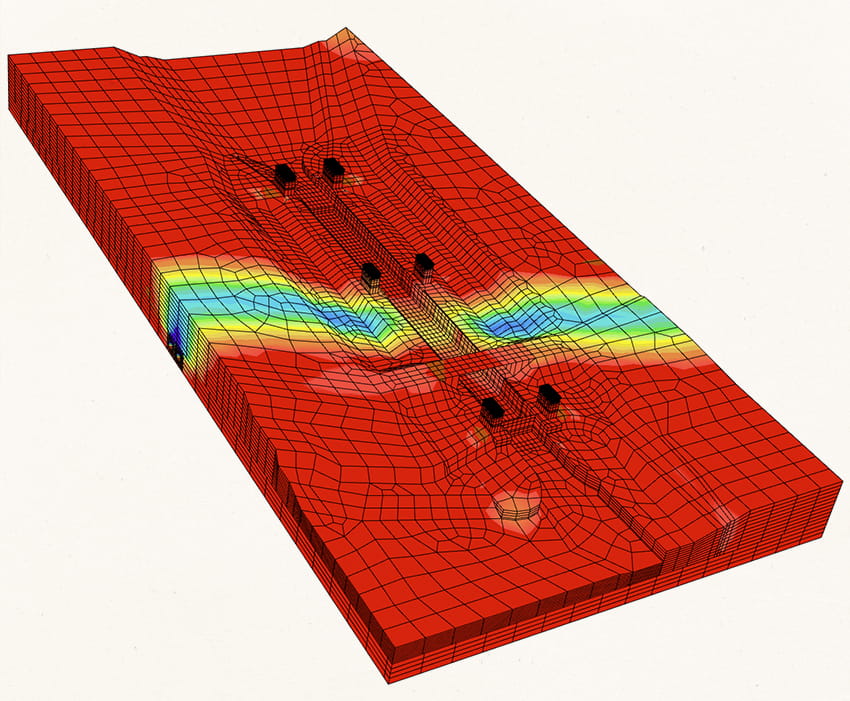


Для создания цифрового двойника ГТС обычно необходимо следующие три вида компьютерного моделирования методом конечных элементов.
1. Прочностное моделирование позволяет определить параметры напряженно-деформированного состояния сооружения и основания.
Исходными данными для прочностной конечно-элементной модели являются:
— физико-механические характеристики строительных материалов и грунтов;
— опорные закрепления, жесткие или упругие (пружины, коэффициенты постели), а также заданные смещения опор (кинематические граничные условия);
— внешние силы (сосредоточенные или распределенные нагрузки, включая силу тяжести и взвешивание в воде);
— объемные деформации материалов (температурное расширение, усадка и т.п.).
Компьютерный расчет представляет собой решение основного уравнения метода конечных элементов, записываемого в матричной форме:
[K]·{u} = {p}
где [K] — матрица жесткости, которая является компьютерным представлением сетки конечных элементов и свойств материалов;
{u} — вектор-столбец перемещений узлов;
{p} — вектор-столбец внешних сил, приложенных к узлам.
Таким образом, все нагрузки и воздействия в ходе компьютерного моделирования преобразуются к сочетанию заданных внешних сил, приложенных к узлам, и заданных перемещений узлов (частный случай перемещения – это опорное закрепление, т.е. перемещение, заданное равным 0).
Рассмотренная формула представляет собой систему линейных алгебраических уравнений (СЛАУ). Ее размерность зависит от количества узлов и количества степеней свободы в каждом узле.
При моделировании грунта в двухмерной (плоскоприведенной) постановке в каждом узле по 2 степени свободы (перемещения по осям координат X и Y), в трехмерной (пространственной) постановке – по 3 степени свободы (перемещения по осям координат X, Y и Z).
При моделировании изгибаемых конструкций (балочных, плитных) в двухмерной постановке в каждом узле 3 степени свободы (перемещения по осям координат X и Y и поворот вокруг оси Z), в трехмерной постановке – 6 степеней свободы (перемещения по каждой оси и повороты вокруг каждой оси).
Таким образом, в двухмерной постановке для одного треугольного конечного элемента (который может применяться для моделирования грунта в постановке плоской деформации) количество узлов 3, количество степеней свободы в каждом узле 2 (перемещения по осям X и Y), количество степеней свободы 3·2 = 6, размерность матрицы жесткости 6×6, получится 6 уравнений:
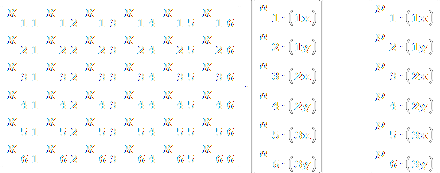
где Kij – элементы матрицы жесткости (i – индекс строк, j – индекс столбцов);
ui – перемещения узлов в направлении степени свободы под порядковым номером i (для примера в скобках даны соответствующие каждой степени свободы номера узлов и направления перемещения);
pi – внешние силы или опорные реакции, приложенные по степени свободы под порядковым номером i.
Элемент матрицы жесткости Kij численно равен реактивной силе, возникающей в i-ом направлении от единичного перемещения в j-ом направлении. Например, K45 равен силе p4(2y), вызываемой единичным перемещением u5(3x).
Матрица жесткости для всей сетки конечных элементов формируется путем объединения матриц жесткости каждого конечного элемента.
Таким обрзаом, в ходе компьютерного расчета первоначально определяются результаты, связанные с узлами сетки, т.е. перемещения и опорные реакции. Далее по алгоритмам метода конечных элементов вычисляются результаты, распределенные в объеме конечных-элементов: деформации, напряжения и другие необходимые параметры напряженно-деформированного состояния.
В рамках прочностной задачи различают статику и динамику [I.8].
В статике скорость деформации модели полагается бесконечно малой. Поэтому инерционная сила в узле эквивалентна силе тяжести и постоянна во времени:
Fg = m·g
где Fg – сила тяжести;
m – масса;
g = 9,81 м/с2 ускорение свободного падения.
Шкала времени в статическом расчете обозначает последовательность этапов моделирования, при этом размерность шкалы времени и продолжительность временных интервалов между этапами значения не имеют.
Именно в статической постановке проводится большинство прочностных расчетов в области строительства.
В динамике рассматриваются не только перемещения узлов, но также учитывается время, за которое эти перемещения происходят. Таким образом, в основное уравнение метода конечных элементов вводятся скорость и ускорение узлов:
[M]·{ü} + [C]·{u̇} + [K]·{u} = {p}
где [M] — матрица масс;
{ü} — вектор-столбец ускорений узлов;
[C] — матрица демпфирования;
{u̇} — вектор-столбец скоростей узлов.
Ускорение, приобретаемое узлом, в соответствии со вторым законом Ньютона вызывает силу, прямо пропорциональную массе:
F = m·ü
Сила, возникающея в результате движения, суммируется с силой тяжести. В результате равнодействующая инерционная сила становится переменной во времени и может отличаться от силы тяжести по величине и направлению.
Шкала времени в динамическом расчете точно соответствует физическому времени.
Динамика рассматривается в неявной и явной постановке.
В неявной динамике скорость распространения механического взаимодействия в объеме конечно-элементной сетки полагается бесконечно большой. Таким образом, сила, приложенная в определенный момент времени, моментально начинает влиять на все узлы (при этом перемещения, скорости и ускорения в каждом узле начинают изменяться во времени в зависимости от распределения жесткостей, демпфирования и масс, например, в виде колебательного движения).
Шаг во времени в постановке неявной динамики учитывает характерные частоты собственных колебаний сооружения (типичный шаг для строительных сооружений и грунтов составляет десятые или сотые доли секунды).
В постановке неявной динамики проводятся расчеты ГТС на сейсмические воздействия.
В явной динамике учитывается скорость распространения механического взаимодействия, равная скорости распространения упругих волн (скорости звука) в моделируемой среде (грунте, бетоне). Например, опорная реакция на приложенную нагрузку возникает не сразу, а с задержкой на время прохождения упругой волны от места приложения нагрузки до опоры. Таким образом, в явной динамике не применяется привычное условие равновесия, при котором сумма всех сил и моментов в любой момент времени равна нулю.
Требуемый шаг во времени в постановке явной динамики зависит от размеров конечных элементов и соответствует времени прохождения упрругой волны через конечный элемент (типичный шаг для строитльных сооружений и грунтов составляет тысячные доли секунды).
В постановке явной динамики проводятся расчеты ГТС на быстропротекающие воздействия ударного характера, например, на столкновение с самолетом.
2. Фильтрационное моделирование определяет параметры насыщения водой и движения воды в сооружении и основании (часто – только в основании).
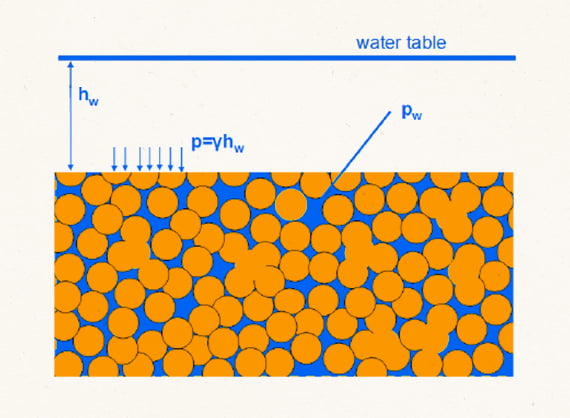
Исходными данными для фильтрационной конечно-элементной модели являются:
— фильтрационные характеристики материалов (коэффициент фильтрации, пористость, коэффициент остаточной водонасыщенности);
— напоры воды (граничные условия первого рода), например, напор на дно водоема;
— фильтрационные расходы (граничные условия второго рода), например, водопонижение с фиксированным расходом откачки;
— расходы, зависящие от напора (граничные условия третьего рода), например, поверхность высачивания.
В ходе компьютерного расчета в узлах конечно-элементной сетки определяются напоры воды. Расчет может проводиться в стационарной или нестационарной постановке.
Стационарная постановка предполагает определение установившегося (постоянного во времени) фильтрационного режима. Шкала времени в стационарном расчете обозначает последовательность этапов моделирования, размерность шкалы времени и продолжительность временных интервалов между этапами значения не имеют.
Нестационарная постановка учитывает скорость изменения фильтрационного режима во времени. Например, как скоро поднимется депрессионная поверхность при временном повышении уровня водохранилища, или когда опустится депрессионная поверхность после запуска водопонижения. Соответственно, в нестационарном расчете учитывается время и объемы воды, необходимые для водонасыщения или осушения грунта.
Шкала времени в нестационарном расчете точно соответствует физическому времени. Шаг времени определяется продолжительностью фильтрационного процесса и обычно составляет от суток до декады.
Для нестационарного расчета фильтрации требуется определение начальных условий, в качестве которых обычно используются результаты стационарного расчета для фильтрационного режима, наблюдавшегося в течение долгого периода времени.
Фильтрационный расчет проводится для получения следующих результатов:
— определение противодавления на подошву плотины или давления обводненных грунтов на сооружение;
— определение депрессионной поверхности (изменение уровня грунтовых вод – барражный эффект, недопущение высачивания на низовой грани плотины);
— проверка фильтрационной устойчивости оснований и грунтовых сооружений (скорость фильтрации должна быть ниже допустимой);
— расчет дренажных расходов;
— расчет консолидации грунтов.
3. Моделирование теплообмена воспроизводит температурный режим в сооружении и основании (часто – только в сооружении).
Исходными данными для конечно-элементной модели теплообмена являются:
— физические характеристики материалов (теплопроводность, плотность, удельная теплоемкость);
— температуры (граничные условия первого рода), например, постоянная температура подземной среды;
— тепловые потоки (граничные условия второго рода), например, количество теплоты, выделяемое при экзотермической реакции твердения бетона;
— тепловые потоки, зависящие от температуры (граничные условия третьего рода), например, условия конвекции или лучистого нагрева на поверхности сооружения, контактирующей с воздухом.
В ходе компьютерного расчета в узлах конечно-элементной сетки определяются температуры. Расчет может проводиться в стационарной и нестационарной постановке (аналогично фильтрационному расчету).
Для нестационарного расчета необходимо определение начальных условий. Однако, сезонный температурный режим изменяется постоянно (т.е. не сохраняется в течение продолжительного периода). Это не позволяет задать начальные условия с помощью стационарного расчета. Поэтому нестационарный расчет теплообмена начинают со среднегодовой температуры, и далее ведется расчет за период в несколько лет до тех пор, пока не сформируется температурный режим, совпадающий с данными мониторинга. Полученный температурный режим выполняет роль начальных условий для последующих этапов расчета.
Расчет теплообмена часто необходим для определения температурного поля в бетонных сооружениях при сезонном температурном воздействии. В дальнейшем температурное поле передается в прочностной расчет для учета температурного расширения бетона.
Связное (мультифизичное) моделирование – это совместное использование нескольких видов моделирования для решения общей задачи. В этом случае результаты одного вида моделирования используются в качестве нагрузок и воздействий для другого вида моделирования.
Например, понижение температуры бетона по результатам расчета теплообмена вызывает уменьшение объема бетона в прочностной задаче. Если свобода изменения размера бетонной конструкции ограничена (случай статически неопределимой задачи), это вызовет увеличение растягивающих напряжений и может привести к трещинообразованию и раскрытию швов.
Некоторые типы связных расчетов имеют традиционные названия:
— двухфазный расчет – это связный расчет прочности и фильтрации;
— расчет термоупругости – это связный расчет прочности и теплообмена;
— расчет тепломассопереноса – это связный расчет фильтрации и теплообмена.
Для разработки цифрового двойника ГТС обычно требуется связный расчет прочности, фильтрации и теплообмена.
Связная модель может иметь как одну сетку конечных элементов, которая используется для всех видов моделирования, так и несколько сеток, предназначенных для разных видов моделирования. Использование нескольких сеток целесообразно в случае противоречий между видами моделирования по требованиям к густоте конечно-элементной сетки в разных областях модели.
1.1.2. Напряженно-деформированное состояние (НДС) – это совокупность параметров, характеризующих состояние сооружения под действием нагрузок и воздействий. Основными параметрами являются:
— перемещения и повороты;
— напряжения;
— деформации.
Чтобы определить параметры напряженно-деформированного состояния с высокой точностью в строго определенных контрольных точках сооружения необходимо учесть местоположение этих точек при разработке сетки конечных элементов.
Возможно определение различных специализированных параметров для инженерного анализа, например:
— давление на контакте сооружения с основанием, величина раскрытия и длина сдвига по контакту;
— внутренние усилия в изгибаемых конструкциях, таких как перекрытия или «стены в грунте» (изгибающий момент, продольная и поперечная сила);
— усилия в фактически установленной арматуре.
Возможность определения специализированных параметров должна быть учтена при разработке сетки конечных элементов.
Анализ результатов напряженно-деформированного состояния требует четкого выбора системы координат. Обычно принимается следующая глобальная система координат:
— ось X направлена вдоль потока;
— ось Y направлена вверх;
— ось Z направлена от левого берега к правому.
Результаты представляются, как правило, в глобальной системе координат. Иногда необходимо введение локальных систем координат (например, для конструкции цилиндрической формы, такой как кожух генератора в здании ГЭС). В таких случаях система координат оговаривается особо.
Перемещения и повороты представляют собой векторные величины, которые определяют как абсолютное значение результата, так и его направление в пространстве (вектор поворота направлен перпендикулярно плоскости вращения по правилу правой руки). Обычно рассматриваются компоненты векторов по осям координат X, Y, Z.
Напряжения представляют собой тензорную величину, которая определяет комбинацию взаимосвязанных векторов напряжений. Тензор напряжений состоит из 6 компонент:
— три компоненты нормальных напряжений: σx, σy, σz;
— три компоненты касательных напряжений: τxy, τyz, τxz.
Для нормальных напряжений принято следующее правило знаков: положительные напряжения – растягивающие, отрицательные напряжения – сжимающие.
Численные значения компонент тензора зависят от выбора системы координат. Причем существует такая система координат, при выборе которой касательные напряжения становятся равными нулю, а нормальные напряжения принимают экстремальные значения. Такие нормальные напряжения называются главными:
σ1 ≥ σ2 ≥ σ3,
где σ1 – наибольшее (с учетом правила знаков) нормальное напряжение в исследуемой точке, σ3 – наименьшее нормальное напряжение.
Таким образом, направление нормальных напряжений σx, σy и σz во всех конечных элементах одинаково (в соответствии с выбранной системой координат). Направление главных напряжений σ1, σ2 и σ3 в каждом конечном элементе индивидуально и не зависит системы координат.
Инвариант тензора – это скалярная величина, которая остается постоянной при выборе любой системы координат. Например, первый инвариант тензора напряжений вычисляется следующим образом:
I1 = σ1 + σ2 + σ3= σx + σy + σz = 3·σ0,
где σ0 – среднее напряжение.
Тензор напряжений Tσ может быть разложен на два тензора:
— шаровой тензор Tσ0, характеризующий изменение объема материала (от действия напряжений равномерного сжатия или растяжения, равных σ0);
— девиатор Dσ, характеризующий искажение формы материла.
Второй инвариант девиатора вычисляется следующим образом:
J2= 0.5·[(σ1 – σ0)2 + (σ2 – σ0)2 + (σ3 – σ0)2] =
= (1/6)·[(σx – σy)2 + (σy – σz)2 + (σz – σx)2 + 6·(τxy2 + τyz2 + τxz2)]
В геотехнике используются следующие инварианты [I.5]:
p = -I1 / 3
q = (3·J2)0.5
Таким образом, напряженное состояние может быть представлено многими путями, в зависимости от контекста инженерной задачи:
— в виде нормальных и касательных напряжений по осям координат X, Y, Z;
— в виде главных напряжений с указанием направлений их действия;
— в виде инвариантов напряжений.
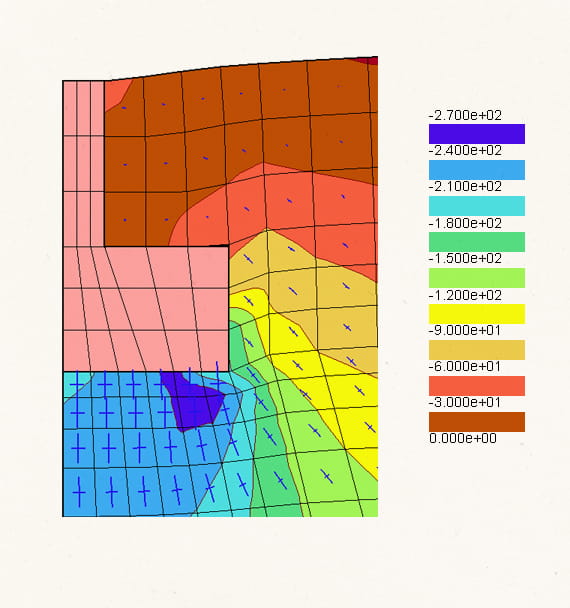
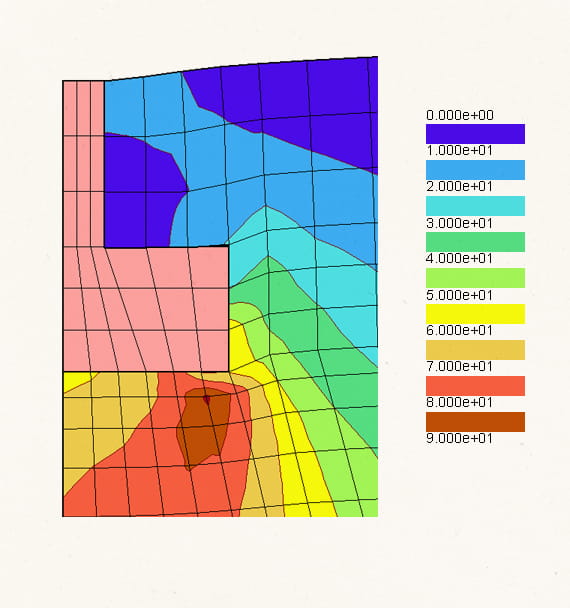
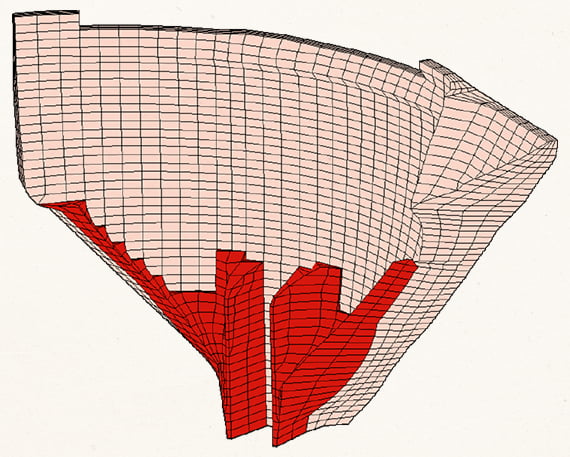
1.1.3. История сооружения при разработке цифрового двойника – это последовательность этапов строительства и приложения нагрузок и воздействий, что представляет собой генетическую нелинейность 1.1.4. Важность ее учета можно проиллюстрировать на примере плотины.
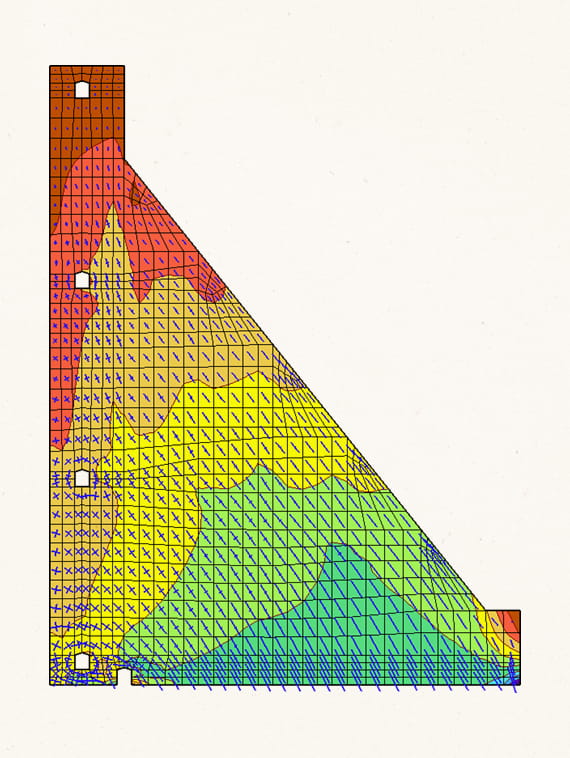
Неравномерность напряжений при учете поэтапности вызвана нагружением плотины до завершения ее возведения. На каждом этапе нагрузка передается только на возведенную часть плотины. При этом отдельные области плотины (например, низовая сторона первого столба) нагружаются сильнее (чем при такой же нагрузке, приложенной к полностью возведенной плотине).
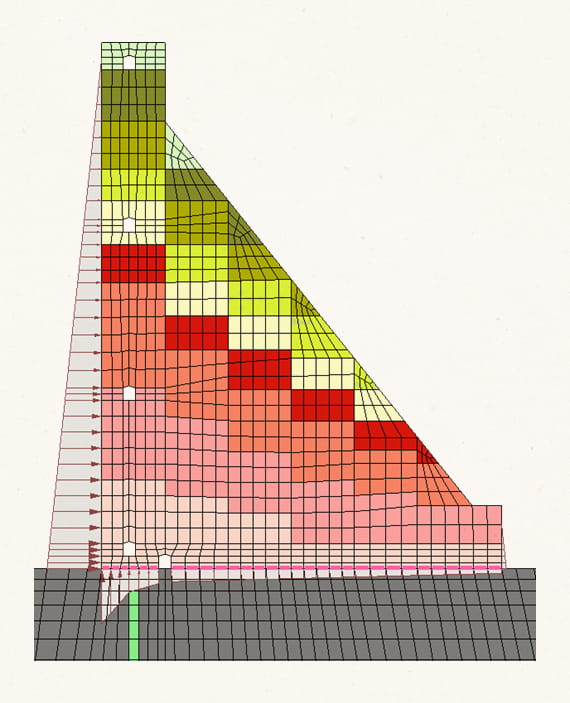
Это явление геометрической нелинейности можно проиллюстрировать на примере консоли с промежуточной опорой. Консоль нагружается за два этапа: до промежуточной опоры, и выше промежуточной опоры. Общая высота консоли 9 м, промежуточная опора на 2/3 высоты. Равномерно-распределенная нагрузка 100 кН/м.
В первом варианте промежуточная опора вводится сразу (мгновенное возведение). Во втором варианте – после первого этапа нагрузки (поэтапное возведение).
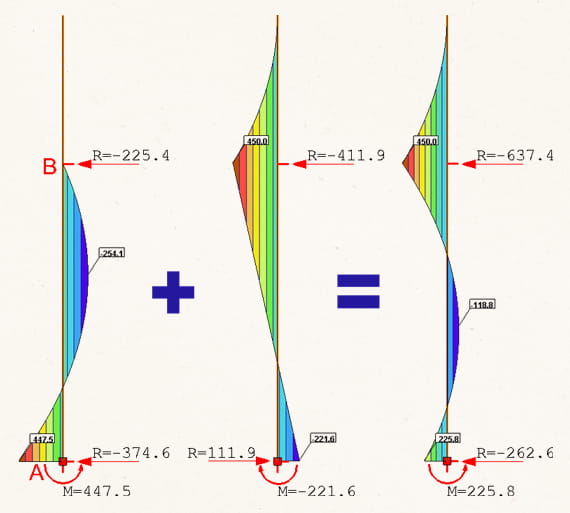
В случае мгновенного возведения при нагружении ниже промежуточной опоры расчетная схема представляет собой жестко защемленную консоль высотой l1 с опорой. Параметры напряженно-деформированного состояния могут быть определены по формулам:
— изгибающий момент в пролете M = 9·q·l12 / 28;
— изгибающий момент в заделке MA = q·l12 / 8;
— опорная реакция на верхней опоре RA = 5·q·l12 / 8;
— опорная реакция в заделке RB = 3·q·l12 / 8.
Полное нагружение можно представить по принципу суперпозиции как сумму нагружения нижней и верхней частей консоли. При этом от нагрузки на верхнюю часть консоли на промежуточной опоре возникает изгибающей момент MB = q·l22 / 2.
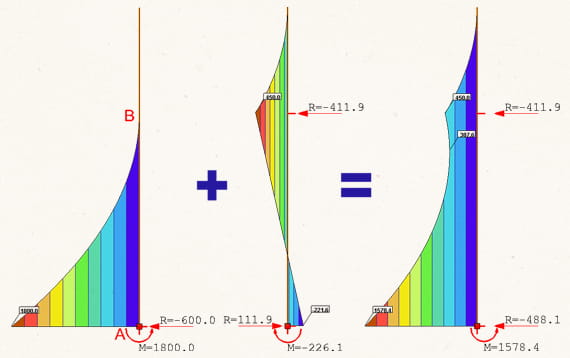
В случае поэтапного возведения при нагружении нижней части консоли расчетная схема представляет собой жестко защемленную консоль высотой l1. Опора сверху отсутствует. Параметры напряженно-деформированного состояния могут быть определены по формулам:
— изгибающий момент в заделке MA = q·l12 / 2;
— опорная реакция в заделке RA = q·l1;
Полное нагружение также можно представить по принципу суперпозиции. При этом расчетная схема нагружения верхней части консоли учитывает промежуточную опору и в точности соответствует рассмотренному выше случаю мгновенного возведения.
Сопоставление результатов покрывает, что учет поэтапного введения промежуточной опоры оказывал определяющее влияние на результат расчета напряженно-деформированного состояния:
– в случае мгновенного возведения нагрузка на нижнюю часть консоли распределилась между точками А и В;
– в случае поэтапного введения промежуточной опоры нагрузка на нижнюю часть консоли полностью воспринята точкой А;
– при нагружении верхней части консоли приращение параметров напряженно-деформированного состояния одинаково в обоих случаях (потому что после введения промежуточной опоры расчетная схема нагружения верхней части консоли одинакова).
Таким образом, влияние поэтапности (геометрической нелинейности) проявляется в эффекте «запоминания» напряженно-деформированного состояния в момент приложения нагрузки. Новые элементы расчетной схемы не разгружают ранее созданные элементы от действия ранее приложенных нагрузок.
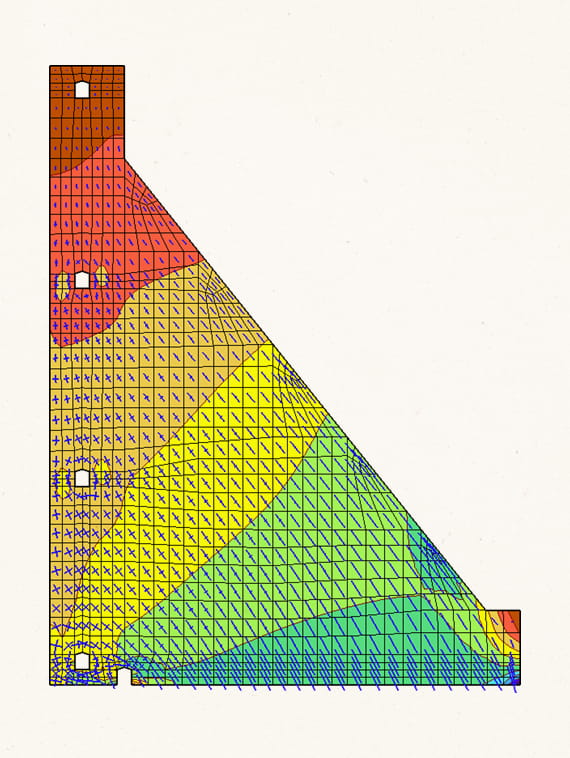
В рассмотренном примере консоль аналогична первому столбу плотины, а промежуточная опора аналогична опиранию первого столба на второй столб.
При опережающем наполнении водохранилища первый столб возвышается над вторым столбом и нагружается по консольной схеме. Возникшие при этом напряжения в первом столбе не разгружаются после достройки второго столба.
Поскольку второй столб возводится позже, его напряженно-деформированное состояние определяется не всей гидростатической нагрузкой, а приращением нагрузки после возведения и набора прочности соответствующих блоков бетонирования второго столба.
Этот эффект возникает при каждом подъеме водохранилища и между каждой парой столбов. Поэтому с низовой стороны столбов формируется зона повышенного сжатия.
Таким образом, поэтапность возведения сооружения и приложения нагрузок в большинстве случаев оказывает значительное влияние на напряженно-деформированное состояние сооружения, что требует учета поэтапности при разработке цифрового двойника.
1.1.4. Нелинейность напряженно-деформированного состояния – это явление, при котором реакция сооружения (перемещения, деформации, напряжения) перестает быть прямо пропорциональной нагрузкам и воздействиям. Это означает, что свойства сооружения непостоянны и в свою очередь зависят от нагрузок и воздействий. Учет этого оказывает определяющее влияние на точность компьютерного моделирования.
Различают следующие виды нелинейности [I.2, I.5]:
— генетическая – моделирование поэтапности возведения сооружения и поэтапности приложения нагрузок и воздействий;
— конструктивная – моделирование взаимодействия частей сооружения между собой, например, раскрытие и сдвиг по контакту сооружения с основанием;
— физическая – учет изменения прочностных и деформационных свойств материалов в зависимости от напряженного состояния;
— геометрическая – учет деформированной геометрии сооружения при расчете напряженно-деформированного состояния.
В рамках компьютерного моделирования возникает понятие инженерной нелинейности, что обозначает различные инженерные приемы, направленные на понижение степени нелинейности расчетной схемы, вплоть до ее линеаризации, при косвенном учете нелинейности благодаря подбору эффективных (приведенных) свойств материалов. К такому приему можно отнести снижение модуля деформации железобетона с учетом трещинообразования.
1. Генетическая нелинейность рассмотрена выше при учете поэтапности 1.1.3 возведения сооружения и приложения нагрузок.
2. Конструктивная нелинейность часто выражается во взаимодействии по контакту сооружения с основанием, что предполагает:
— возможность раскрытия по контакту, т.е. отлипание сооружения от основания;
— возможность сдвига по контакту, т.е. проскальзывание сооружения по основанию.
Контактное взаимодействие учитывается путем включения в компьютерную модель контактных конечных элементов. Эти элементы разделяют сетку конечных элементов на части (по одну и другую сторону контакта), создавая возможность взаимного смещения частей сетки конечных элементов.
Поверхности, на которых возможно проявление контактного взаимодействия (раскрытие контакта, сдвиг по контакту), должны быть определены при разработке модели, чтобы в сетке конечных элементов были предусмотрены соответствующие контактные элементы.
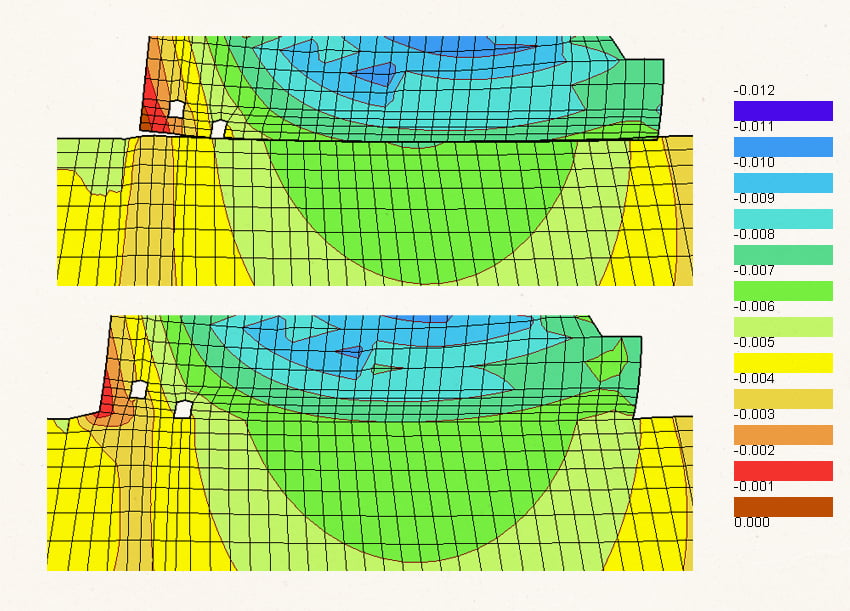
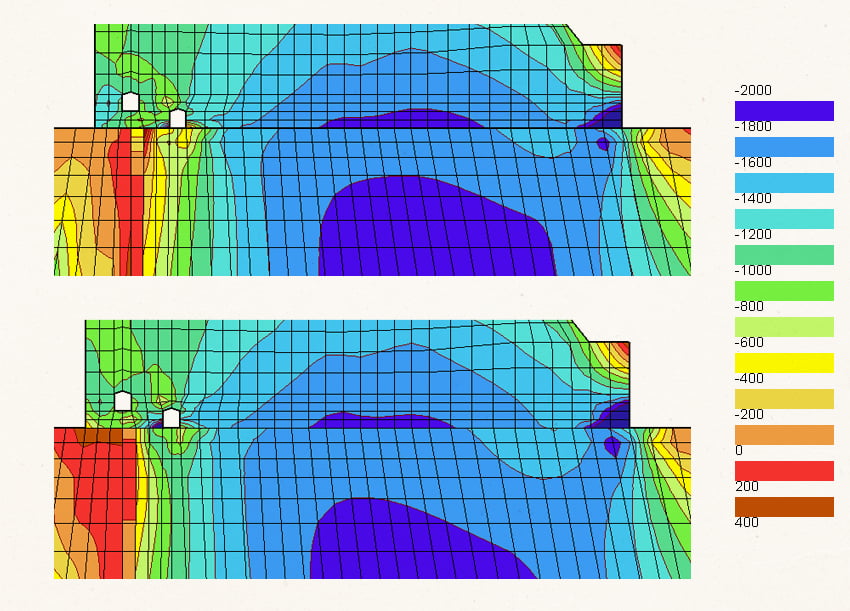
Под действием гидростатической нагрузки контакт плотины с основанием под верховой гранью разуплотняется.
Без учета контактного взаимодействия сооружение прилипает к основанию, в результате чего основание удерживает плотину от смещения: в основании под верховой гранью возникают растягивающие напряжения, а перемещения плотины уменьшаются.
Таким образом, контактное взаимодействие плотины с основанием необходимо учитывать при разработке цифрового двойника.
3. Физическая нелинейность связана с упругопластическим характером работы материалов (упругая составляющая деформации обратима, т.е. исчезает после снятия нагрузки, пластическая составляющая деформации необратима, т.е. сохраняется после снятия нагрузки). В результате проявления пластических деформаций:
— возникает перераспределение напряжений, когда материал легче деформируется и дальнейшее приращение нагрузки передается на смежные менее напряженные области;
— происходит упрочнение материала, т.е. в случае снятия нагрузки материал будет работать упруго до возвращения к ранее достигнутому уровню нагрузки.
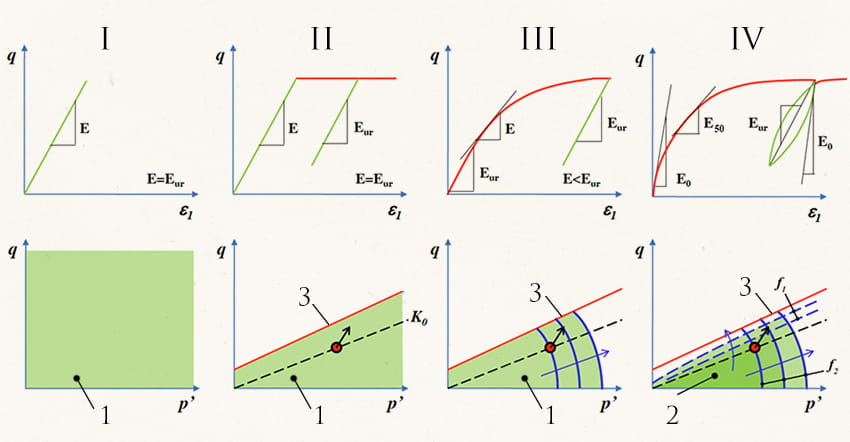
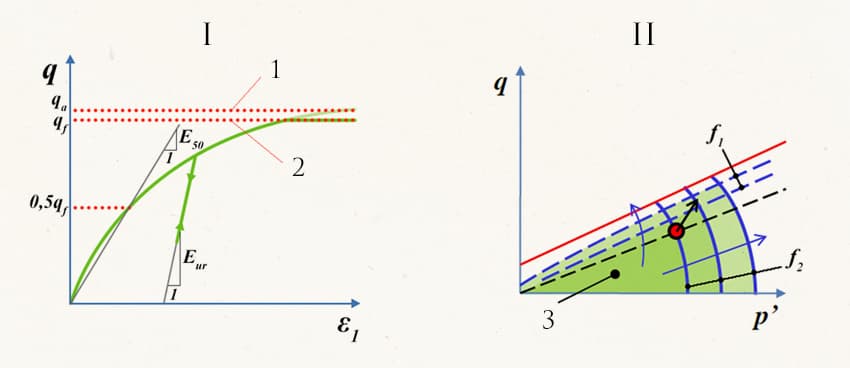
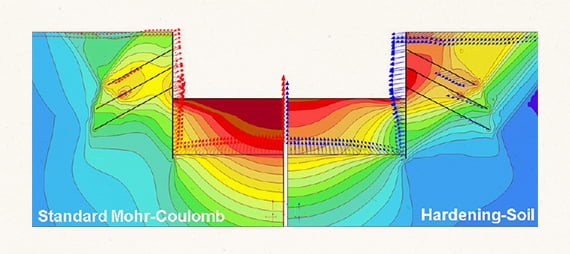
Особенно сильно физическая нелинейность проявляется для оснований. Для компьютерного моделирования физической нелинейности разработаны специальные модели материалов. В настоящее время наиболее точными считаются модели:
— Hardening Soil для дисперсных грунтов [I.9, I.10, I.11, I.12, I.13];
— Hoek-Brown для скальных грунтов [I.14, I.15, I.16].
В результате упрочнения модуль деформации грунта при первоначальном нагружении становится меньше модуля деформации при разгрузке и последующем нагружении (например, при колебаниях уровня воды в водохранилище).
После снятия нагрузки грунт работает с более высоким модулем деформации вплоть до возвращения к ранее достигнутому уровню нагрузки. Это явление проявляется в том числе в результате переуплотнения грунтов в ходе геологической истории.
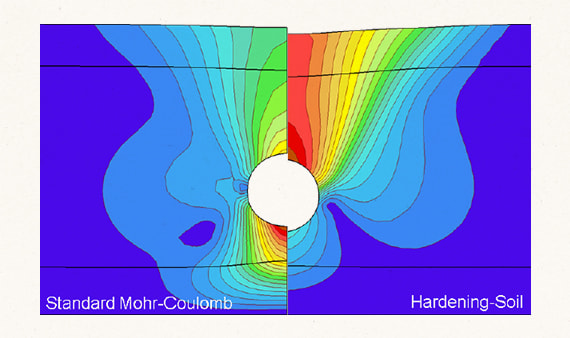
Учет переуплотнения и упрочнения грунта по модели Hardening Soil во многих случаях значительно повышает точность расчета вертикальных перемещений проектируемого сооружения и существующих сооружений, расположенных в пределах мульды осадок.
Для нелинейного моделирования бетона применяется модель упруго-поврежденно-пластического материала CPDM (Concrete Plastic Damage Model) [I.17].
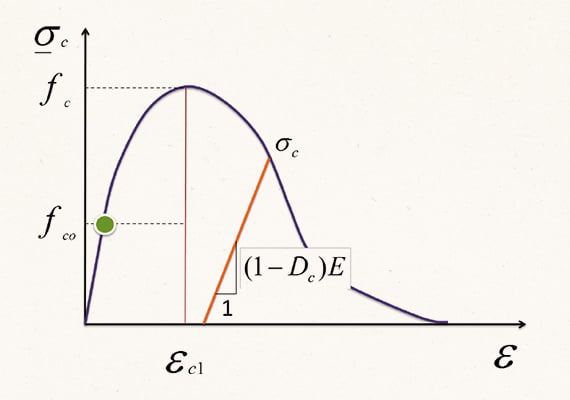
С точки зрения компьютерного моделирования, модель материала представляет собой алгоритм, вычисляющий жесткость конечных элементов.
Основой модели материала является критерий прочности, который идентифицирует состояние материала (упругое, пластическое с упрочнением, пластическое течение) в условиях пространственного напряженного состояния (например, при всестороннем обжатии). Таким образом, в каждом конечном элементе состояние материала определяется индивидуально и уточняется на каждом расчетном этапе.

4. Геометрическая нелинейность проявляется при обновлении геометрических размеров сооружения с учетом возникших перемещений и деформаций. В компьютерном моделировании это называется учетом «больших перемещений» [I.18].
Влияние геометрической нелинейности показано на следующем примере, где колонна высотой H = 6,0 м загружена вертикальной и горизонтальной нагрузкой.
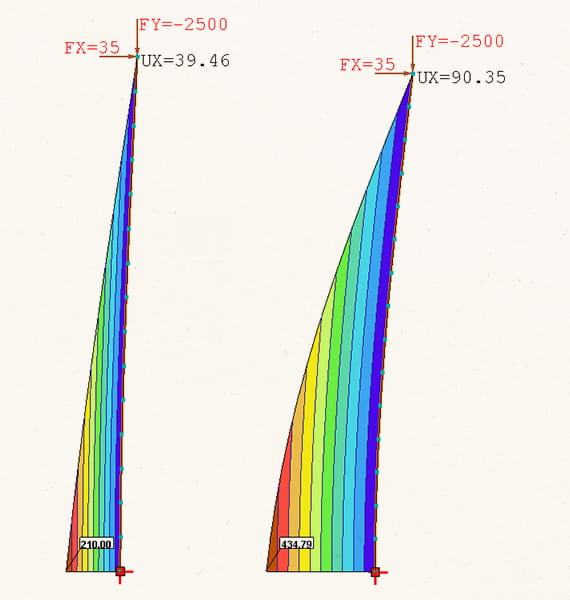
В линейном расчете изгибающий момент в заделке 210 кН·м, горизонтальное перемещение 39,46 мм. Этот результат может быть получен аналитически по формулам
M = FX·H,
f = FX·H3 / (3·E·I),
где E·I – жесткость колонны, принятая 6,4·104 кН·м2.
Однако горизонтальное перемещение верха колонны вызывает смещение опорной площадки для вертикальной нагрузки. От этого возникает дополнительный изгибающий момент FY·UX, усиливающий действие горизонтальной нагрузки.
В результате геометрически нелинейного расчета изгибающий момент в заделке и горизонтальное перемещение верха колонны увеличиваются более чем в два раза.
Обычно геометрическая нелинейность наиболее сильно проявляется при расчете строительных конструкций, таких как колонны, балки, плиты.
Учет различных видов нелинейности значительно повышает достоверность компьютерного моделирования, поэтому имеет большое значение для разработки цифровых двойников.
1.2.1. Отличия цифрового двойника от компьютерных моделей, применяемых на стадии проектирования, представлены в таблице.
Сопоставление цифрового двойника с компьютерной моделью при проектировании
|
Цифровой двойник |
Компьютерная модель на стадии проектирования |
|
Моделирует существующее сооружение (эксплуатируемое или на этапе строительства) |
Моделирует будущее сооружение |
|
Фактические свойства материалов и грунтов (эффективные*, с учетом масштабного эффекта**) известны приблизительно (например, модуль деформации грунта) |
Свойства материалов и грунтов принимаются по нормам проектирования |
|
Фактические нагрузки и воздействия известны точно (например, уровень воды в водохранилище) или приблизительно (например, противодавление на подошву плотины) |
Нагрузки и воздействия принимаются в соответствии с нормами проектирования |
|
Модель работает с любыми сочетаниями нагрузок и воздействий, возможными для сооружения |
Модель работает с заранее известным перечнем проектных сочетаний нагрузок и воздействий |
|
Модель используется многократно (сотни и тысячи запусков) в течение продолжительного периода времени (от месяцев до десятков лет) |
Модель используется на этапе проектирования |
|
Состояние сооружения по результатам моделирования должно точно соответствовать действительному |
Состояние сооружения по результатам моделирования должно быть не более благоприятным, чем в действительности |
|
Необходим учет нелинейности для обеспечения требуемой точности моделирования |
Необходимость учета нелинейности определяется расчетной схемой |
|
Точность модели оценивается по соответствию данным мониторинга |
Точность модели оценивается экспертным путем по соответствию нормам и опыту проектирования |
|
Коэффициенты надежности по нагрузкам, свойствам материалов и т.п. не используются |
Используются коэффициенты надежности, установленные нормами проектирования |
** Масштабный эффект – это тенденция к ухудшению некоторых свойств реального сооружения по сравнению с лабораторным образцом материала по причине влияния случайных дефектов, количество которых тем больше, чем больше размер сооружения
Таким образом, цифровой двойник должен точно соответствовать особенностям реального сооружения, которые в проекте не установлены и могут быть неизвестны. Поэтому при разработке III цифрового двойника необходимо уточнение исходных данных, в частности:
— путем моделирования лабораторных испытаний для повышения точности оценки физико-механических характеристик [I.19];
— путем машинного обучения 3.1 компьютерной модели по данным мониторинга.
1.2.2. Нормы проектирования регламентируют учитываемые нагрузки и воздействия, а также их сочетания, в целях обеспечения надежности и безопасности сооружения. При проектировании учитываются наиболее неблагоприятные (максимальные или минимальные) значения нагрузок и их сочетаний, возможные в течение срока эксплуатации объекта.
В различных расчетах могут учитываться различные численные значения одной и той же нагрузки, причем эти значения могут различаться по нормам проектирования разных стран. Различают следующие значения нагрузок:
— нормативные (базовые) значения – это наиболее неблагоприятное значение нагрузки с определенной вероятностью непревышения в течение срока службы сооружения (или иного периода времени, например, 1 год, 5 лет или 10000 лет);
— расчетные значения – это нормативные значения, умноженные на коэффициент надежности по нагрузке, который зависит от вида расчета и обычно равен единице при расчете деформаций, прогибов и перемещений, и обычно больше единицы при расчете прочности и устойчивости.
Подобным образом различаются нормативные и расчетные характеристики материалов, и вводится коэффициент надежности по материалу (по грунту).
Используются и другие коэффициенты, например, коэффициент сочетания нагрузок и коэффициент надежности по ответственности.
Таким образом, при проектировании различные параметры напряженно-деформированного состояния определяются при различных численных значениях как нагрузок, так и свойств материалов.
Поэтому определяемые при проектировании параметры напряженно-деформированного состояния сооружения не соответствуют реальным физически обусловленным параметрам, которые измеряются в ходе мониторинга. Это затрудняет анализ результатов мониторинга и обуславливает различия между цифровыми двойниками и компьютерными моделями других типов, которые используются при проектировании.
1.3.1. Цифровой двойник предназначен для точного определения напряженно-деформированного состояния сооружения в любой момент времени, что требует точных данных о фактических нагрузках и воздействиях. Однако, не все виды нагрузок и воздействий поддаются регистрации системой мониторинга в явном виде. В таких случаях требуется их уточнение путем перекрестного анализа данных различных натурных измерений.
Например, гидростатическое давление на верховую грань плотины известно точно (при известном уровне верхнего бьефа). В то же время, противодавление на подошву плотины известно приблизительно, потому что эпюра противодавления зависит от фильтрационного режима основания и сплошности противофильтрационной завесы. Для уточнения фактического противодавления используются данные напорных и безнапорных пьезометров.
I.1) ↑ Bathe K-J (2016) Finite Element Procedures. Second Edition. (Download PDF)
I.2) ↑ Reddy J N (2015) An Introduction to Nonlinear Finite Element Analysis with Applications to Heat Transfer, Fluid Mechanics, and Solid Mechanics. Second Edition https://books.google.com/books?id=6k5VBQAAQBAJ
I.3) ↑ Zienkiewicz O C, Taylor R L and Fox D D (2014) The Finite Element Method for Solid and Structural Mechanics. 7th Edition. https://books.google.com/books?id=gTATAAAAQBAJ
I.4) ↑ Hughes T J R (2000) The Finite Element Method: Linear Static and Dynamic Finite Element Analysis. https://books.google.com/books?id=cHH2n_qBK0IC
I.5) ↑ Commend S, Kivell S, Obrzud R, Podleś K, Truty A and Zimmermann Th (2018) Computational Geomechanics. Getting Started with ZSoil.PC. (Download PDF)
I.6) ↑ Urbanski A (2015) Numerical Modeling of Thermal, Filtration and Mechanical Phenomena in a Selected Section of a Gravity Dam. Numerics in Geotechnics and Structures: 93-108. (Download PDF)
I.7) ↑ Mellal A (2015) Seismic Safety of a Buttress Dam and Appurtenant Structures – 3D Static and Dynamic Analyses. Numerics in Geotechnics and Structures: 59-73. (Download PDF)
I.8) ↑ Truty A, Zimmermann Th (2018) Dynamics in ZSoil.PC. ZSoil.PC Report. (Download PDF)
I.9) ↑ Obrzud R, Truty A (2014) The Hardening Soil Model – a Practical Guidebook. ZSoil.PC Report. (Download PDF)
I.10) ↑ Cudny M, Truty A (2020) Refinement of the Hardening Soil model within the small strain range. Acta Geotechnica, 15: 2031-2051. DOI: 10.1007/s11440-020-00945-5. (Download PDF)
I.11) ↑ Truty A, Obrzud R F (2015) Improved Formulation of the Hardening Soil Model in the Context of Modeling the Undrained Behavior of Cohesive Soils. Studia Geotechnica et Mechanica, 37 (2): 61-68. DOI: 10.1515/sgem-2015-0022. (Download PDF)
I.12) ↑ Obrzud R F (2010) On the use of the Hardening Soil Small Strain model in geotechnical practice. Numerics in Geotechnics and Structures: 15-32. (Download PDF)
I.13) ↑ Schanz T, Vermeer P A and Bonnier P G (1999) The Hardening Soil Model: Formulation and Verification. Beyond 2000 in Computational Geotechnics: 281-296. (Download pdf)
I.14) ↑ Truty A, Zimmermann Th. (2014) Hoek-Brown Model for Rocks. ZSoil.PC Report. (Download PDF)
I.15) ↑ Hoek E, Brown E T (2018) The Hoek-Brown Failure Criterion and GSI – 2018 Edition. Journal of Rock Mechanics and Geotechnical Engineering, 11 (3): 445-463. DOI: 10.1016/j.jrmge.2018.08.001. (Download PDF)
I.16) ↑ Hoek E T (2007) Practical Rock Engineering. (Download PDF)
I.17) ↑ Truty A (2018) Elastic-Plastic Damage Model for Concrete. ZSoil.PC Report. (Download PDF)
I.18) ↑ Truty A, Urbanski A and Zimmermann Th (2018) Large Deformation. ZSoil.PC Report. (Download PDF)
I.19) ↑ Obrzud R F, Truty A and Podleś K. with contribution by Commend S and Zimmermann Th (2018) Virtual Lab. ZSoil.PC Report. (Download PDF)
Цифровой двойник применяется в процессе мониторинга сооружений для раннего оповещения о возникновении деструктивных процессов 2.1 , что обеспечивает:
а) предотвращение аварий 2.2;
б) снижение затрат 2.3 на устранение повреждений сооружения за счет их раннего обнаружения;
в) оптимизацию плановых затрат 2.4 на ремонт;
г) уменьшение издержек на страхование благодаря снижению технических рисков.
2.1. Типичное применение цифрового двойника предполагает многократное моделирование фактического состояния сооружения путем добавления в модель новых расчетных этапов, учитывающих изменение нагрузок и воздействий со временем.
Результаты моделирования сопоставляются с показаниями контрольно-измерительной аппаратуры (КИА). Совпадение результатов моделирования и мониторинга означает, что модель сохраняет соответствие реальному сооружению. Поскольку модель не изменялась, значит и состояние сооружения стабильно.
Таким образом, цифровой двойник выявляет суффозию основания, трещинообразование бетона, коррозию арматуры и другие деструктивные процессы благодаря их влиянию на параметры напряженно-деформированного состояния сооружения, прежде всего, на осадки и крены 2.1.1, которые в режиме реального времени могут эффективно контролироваться автоматизированными гидростатическими нивелирами компании Монитрон.
2.2. Цифровой двойник в результате моделирования сооружения, например, может индивидуально для каждого датчика автоматизированного нивелирования (чья точность 0,1 мм) установить прогнозный коридор вертикальных перемещений 2.2.1 и обновлять его по ходу изменения нагрузок и воздействий. Это позволяет обнаружить деструктивные процессы раньше, чем традиционные критерии безопасности 2.2.2, что увеличивает резерв времени для осуществления мер по предотвращению возможной аварии.
2.3. Своевременное обнаружение 2.3.1 деструктивных процессов в большинстве случаев позволяет предложить более экономичное решение по восстановлению состояния сооружения, пока объем накопленных дефектов и повреждений минимален (при более позднем реагировании необходимые затраты обычно возрастают многократно).
2.4. Сопоставительный анализ данных цифрового двойника и результатов мониторинга позволяет ранжировать участки сооружения по стабильности технического состояния, что дает возможность повысить технико-экономическую эффективность 2.4.1 планово-предупредительных ремонтов.
2.1.1. Измерение осадок (вертикальных перемещений) и кренов (углов поворота контролируемых сечений) с помощью датчиков автоматизированного нивелирования позволяет обнаружить деструктивные процессы, входящие в типовые сценарии гидротехнических аварий [II.1, II.2, II.3, II.4, II.5], в частности:
— суффозию основания;
— нарушение сплошности противофильтрационной завесы;
— трещинообразование бетона;
— раскрытие рабочих швов бетонирования;
— коррозию арматуры подпорных стен и других конструкций.
2.2.1. Прогнозный коридор осадок – это расчетное значение осадки на датчике автоматизированного нивелирования по данным цифрового двойника с поправкой на погрешность инженерных расчетов и натурных измерений [II.6]. В силу изменения нагрузок, воздействий и условий эксплуатации прогнозный коридор, как и натурная осадка, изменяется по ходу календарного времени.
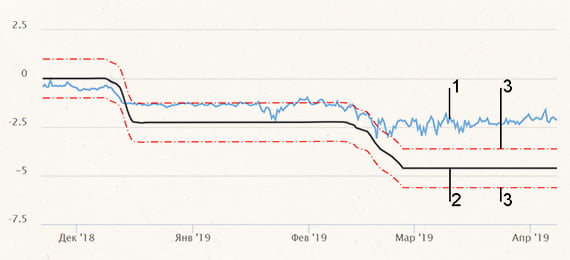
2.2.2. Обычно для анализа результатов мониторинга ГТС используются заранее назначенные критерии безопасности [II.7, II.8, II.9, II.10, II.11], т.е. предельно допустимые значения проектных критериев осадок или других показателей напряженно-деформированного состояния сооружения. Недостатком системы критериев безопасности является то, что они не прогнозируют динамику изменения технического состояния сооружения. До тех пор, пока критерии безопасности не нарушены, сооружение считается работоспособным, даже при тенденции к нарушению критериев безопасности в будущем.
Преимущество цифрового двойника в том, что он анализирует характер развития осадок. Например, по данным мониторинга осадки уменьшаются (происходит подъем), а по данным цифрового двойника осадки должны увеличиваться. Такой пример может указывать на прорыв противофильтрационной завесы и повышение противодавления.
Нарушение нормального тренда осадок произойдет раньше, чем будет нарушен критерий безопасности. Таким образом, цифровой двойник позволяет раньше обнаружить нарушение технического состояния сооружения, чтобы выиграть время для восстановления технического состояния сооружения и предотвращения возможной аварии.
2.3.1. Практическая ценность цифрового двойника заключается в возможности предиктивного мониторинга, т.е. раннего обнаружения деструктивных процессов [II.6, II.12, II.13, II.14, II.15]. Это достигается благодаря тому, что цифровой двойник контролирует исправность сооружения (стабильность его технического состояния) независимо от изменений нагрузок и воздействий. Эти изменения происходят постоянно (например, сезонные температурные колебания) и создают помехи для обычных приемов инженерного анализа. Цифровой двойник работает следующим образом:
— если динамика натурных осадок укладывается в прогнозный коридор – значит техническое состояние сооружения остается неизменным, не развиваются деструктивные процессы, такие как трещинообразование или суффозия;
— если натурные осадки перестали соответствовать цифровому двойнику – значит в техническом состоянии сооружения произошло изменение.
2.4.1. Технико-экономическая эффективность применения цифрового двойника вытекает из сопоставления с системой критериев безопасности.
Цифровой двойник контролирует стабильность технического состояния сооружения, тогда как критерии безопасности фиксируют признаки гидротехнических аварий. Поэтому цифровой двойник раньше выявляет нарушения технического состояния сооружения.
Таким образом, цифровой двойник работает как инструмент управления финансовыми рисками собственника сооружения, обоснования инвестиций и планирования ремонтов [II.16, II.17, II.18]. В то же время, критерии безопасности является прежде всего инструментом обеспечения общественной безопасности в зоне потенциально возможного воздействия волны прорыва при гидротехнической аварии.
II.1) ↑ Aureli F, Maranzoni A, Petaccia G (2021) Review of Historical Dam-Break Events and Laboratory Tests on Real Topography for the Validation of Numerical Models. Water, 13, 1968. DOI: 10.3390/w13141968. (Download PDF)
II.2) ↑ Clearya P W, Prakasha M, Meada S, Tangb X, Wangb H and Ouyangb S (2012) Dynamic simulation of dam-break scenarios for risk analysis and disaster management. International Journal of Image and Data Fusion, 3(4):333-363. (Download PDF)
II.3) ↑ Charles J A, Tedd P, Warren A (2011) Lessons from historical dam incidents. Environment Agency UK. (Download PDF)
II.4) ↑ Wrachien D D (2009) Dam-break Problems, Solutions and Case Studies. https://books.google.com/books?id=WKkwnwEACAAJ
II.5) ↑ Anderson C, Mohorovic C, Larry Mogck L, Cohen B, Scott G (1998) Concrete Dams Case Histories of Failures and Nonfailures with Back Calculations. U. S. Department of the Interior. Bureau of Reclamation. Dam Safety Office. (Download PDF)
II.6) ↑ Medvedev G M and Khoteev E A (2021) Experience in Effective Changing of the Tunneling Parameters According to the Data of Automated Hydrostatic Levels to Minimize the Impact on the Operating Section of the Moscow Metro (from the Experience of the Organization). J. Phys.: Conf. Ser. 1928 012048. DOI: 10.1088/1742-6596/1928/1/012048. (Download PDF)
II.7) ↑ Good Practice Note on Dam Safety (2020) The World Bank. (Download PDF)
II.8) ↑ Guidelines for Safety Inspection of Dams (2018) Government of India. Central Water Commission. Central Dam Safety Organization. (Download PDF)
II.9) ↑ Dam Safety Guide (2012) Häme Centre for Economic Development, Transport and the Environment. Finland. (Download PDF)
II.10) ↑ Federal Guidelines for Dam Safety (2004) U. S. Department of Homeland Security. Federal Emergency Management Agency (FEMA). (Download PDF)
II.11) ↑ Adamo N, Al-Ansari N, Sissakian V, Laue J and Knutsson S (2021) Dam Safety: Use of Instrumentation in Dams. Journal of Earth Sciences and Geotechnical Engineering, 11 (1): 145-202. DOI: 10.47260/jesge/1115. (Download PDF)
II.12) ↑ Khajavi S H, Motlagh N H, Jaribion A, Werner L C and Holmström J. (2019) Digital Twin: Vision, Benefits, Boundaries, and Creation for Buildings. IEEE Access, 7, 147406-147419. DOI: 10.1109/ACCESS.2019.2946515. (Download PDF)
II.13) ↑ Ye Cong, Butler L, Calka B, Iangurazov M, Lu Qiuchen, Gregory A, Girolami M and Middleton C (2019) A Digital Twin of Bridges for Structural Health Monitoring. 12th International Workshop on Structural Health Monitoring. (Download PDF)
II.14) ↑ Lau FD-H, Butler LJ, Adams NM, Elshafie MZEB and Girolami MA (2018) Real-Time Statistical Modelling of Data Generated from Self-Sensing Bridges. Smart Infrastructure and Construction 171(1), 3-13. DOI: 10.1680/jsmic.17.00023. (Download PDF)
II.15) ↑ Salehi H, Burgueño R (2018) Emerging Artificial Intelligence Methods in Structural Engineering. Engineering Structures, 171, 170-189. DOI: 10.1016/j.engstruct.2018.05.084. Open manuscript: https://www.sciencedirect.com/science/article/abs/pii/S0141029617335526
II.16) ↑ Klinc R and Turk Ž (2019) Construction 4.0 – Digital Transformation of One of the Oldest Industries. Economic and Business Review, 21(3). DOI: 10.15458/ebr.92. (Download PDF)
II.17) ↑ Digital Twin: Towards a Meaningful Framework. Arup, 2019. (Download PDF)
II.18) ↑ Bolton A, Enzer M, Schooling J et al (2018) The Gemini Principles: Guiding Values for the National Digital Twin and Information Management Framework. Centre for Digital Built Britain and Digital Framework Task Group. DOI: 10.17863/CAM.32260. (Download PDF)
Цифровой двойник разрабатывается на основе проекта 3.1 с использованием следующих принципов:
а) реалистичного моделирования 3.2, предполагающего моделирование фактического сооружения вместо его идеализированного проекта;
б) машинного обучения компьютерной модели 3.3 по данным мониторинга реального сооружения, как правило, с использованием датчиков автоматизированного нивелирования компании «Монитрон».
3.1. Для компьютерного моделирования 3.1.1 используются стандартные материалы проекта (чертежи, инженерно-геологические разрезы), а также вся имеющаяся дополнительная информация, уточняющая фактическое состояние сооружения, свойства строительных материалов и грунтов (исполнительная документация, результаты инженерных изысканий, технических обследований, исследований геофизическими методами и т.п.)
3.2. Поскольку цифровой двойник отражает действительное состояние сооружения и точно повторяет его перемещения и деформации, при разработке цифрового двойника учитываются реальные свойства строительных материалов и грунтов, реальные величины нагрузок и воздействий. Избегаются инженерные искажения 3.2.1, например, от применения коэффициентов надежности.
3.3. Машинное обучение необходимо для повышения точности расчета осадок и представляет собой корректировку заложенных в компьютерную модель свойств сооружения и основания исходя из сопоставления результатов моделирования с результатами мониторинга реального сооружения.
Для машинного обучения проводится серия расчетов 3.3.1, в которых свойства сооружения и основания варьируются в допустимых пределах 3.3.2. В результате выявляются фактические свойства, при которых результаты моделирования достаточно точно совпадают с результатами мониторинга.
На современном этапе развития технологий мониторинга ГТС наилучшее обучение 3.3.3 цифровых двойников может быть обеспечено датчиками автоматизированного нивелирования.
3.1.1. Начальные этапы компьютерного моделирования при разработке цифрового двойника соответствует общей методике математического моделирования методом конечных элементов 1.1.1:
— на первом этапе создается геометрическая модель сооружения и основания;
— на втором этапе разрабатывается конечно-элементная сетка;
— на третьем этапе прикладываются нагрузки и воздействия за всю известную историю сооружения.
Дальнейшие этапы компьютерного моделирования специфичны для разработки цифровых двойников:
— четвертый этап – машинное обучение 3.3.1 модели по данным мониторинга;
— пятый этап – интеграция модели в автоматизированную систему мониторинга для дальнейшей работы без постоянного участия человека.
Особое внимание уделяется следующим вопросам.
1. В ходе проектирования цифрового двойника необходимо предусмотреть, чтобы конечно-элементная модель могла обработать весь возможный диапазон изменения нагрузок и воздействий.
Цифровой двойник ГТС обычно представляет собой связную (мультифизичную) модель 1.1.1 предназначенную для нескольких видов компьютерного моделирования методом конечных элементов:
— прочностного моделирования в статической нелинейной постановке;
— фильтрационного моделирования в нестационарной постановке;
— моделирования теплообмена в нестационарной постановке.
В зависимости от особенностей моделируемого объекта, разрабатывается единая сетка конечных элементов для всех видов моделирования, или несколько сеток для разных видов моделирования.
На этапе разработки цифрового двойника важно согласовать планируемые виды компьютерного моделирования с источниками исходных данных (учитывая этапы разработки, калибровки и эксплуатации модели).

2. Выбор программного комплекса для конечно-элементного моделирования. В большинстве случаев предпочтительны программы геотехнической направленности, которые отличаются наилучшими возможностями для моделирования нелинейной работы грунтов (скальных и дисперсных).
Это необходимо потому, что работа грунтов оказывает определяющее влияние на осадки ГТС. Расчетная схема таких объектов (плотины, шлюзы, подпорные стены каналов) представляет собой систему «сооружение – основание». Часто плотины и дамбы возводятся из грунтовых материалов (земляные, каменно-земляные, каменно-набросные). Именно с разрушением грунтов связаны наиболее распространенные сценарии гидротехнических аварий 2.1.1 .
Для разработки цифровых двойников наша компания использует геотехнический программный комплекс Z_Soil (Швейцария) [III.2]. В отдельных случаях возможно применение свободного программного обеспечения (СПО) для конечно-элементного моделирования, например, Code_Aster или CalculiX.
3. Учет различных видов нелинейности 1.4 в частности:
— учет поэтапности строительства;
— учет контактных взаимодействий, таких как контакт «бетон-грунт», раскрывающиеся рабочие швы бетонирования, раскрывающиеся межстолбчатые швы плотины и т.п.;
— использование нелинейных моделей материалов (например, Hardening Soil для дисперсных грунтов [III.3], Hoek-Brown для скальных грунтов[III.4], CPDM для бетона [III.5]).
Для этого сетка конечных элементов предусматривает внутренние границы, выделяющие этапы строительства и местоположение швов, предусмотренных в расчетной схеме.
В методе конечных элементов действует закономерность, что нелинейные модели материалов надежнее работают на сетках из конечных элементов в форме параллелепипедов (гексаэдров).
4. Возможность учета всех видов нагрузок и воздействий, актуальных в течение жизненного цикла сооружения, в рамках расчета напряженно-деформированного состояния, фильтрации, теплообмена.
Для учета нагрузок и воздействий сетка конечных элементов обеспечивает требуемый размеров конечных элементов на площадках приложения нагрузок (для распределенных нагрузок) и требуемое местоположение узлов сетки (для сосредоточенных нагрузок).
5. Возможность моделирования показаний датчиков автоматизированного нивелирования или другой контрольно-измерительной аппаратуры.
Для этого предусматриваются узлы конечно-элементной сетки в точках компьютерной модели, соответствующих местам размещения датчиков на реальном сооружении.
3.2.1. Реалистичное моделирование напряженно-деформированного состояния предполагает минимизацию отклонений компьютерной модели от реального сооружения.
Поэтому на разработку цифровых двойных не распространяются некоторые правила и традиции инженерных расчетов, заведомо приводящие к введению в расчетную схему искажений:
— не применяются коэффициенты надежности, потому что от их введения результаты расчета сооружения становится более неблагоприятным, чем в реальности (в том числе коэффициенты надежности, являющиеся вероятностными коэффициентами пересчета повторяемости климатических нагрузок – во всех случаях предпочтение отдается учету фактического значения нагрузки, которое зарегистрировано системой мониторинга);
— избегаются чрезмерные упрощения расчетной схемы, заведомо ухудшающие результаты расчета сооружения (например, для цифрового двойника предпочтительно уточнение эпюры противодавления по результатам пьезометрических наблюдений, потому что эпюра, принятая по нормам проектирования ГТС, явно завышает противодавление);
— не действует инженерная традиция, согласно которой при любой неопределенности в исходных данных или расчетной схеме выбирается наиболее неблагоприятный вариант (вместо этого при разработке цифрового двойника неопределенность разрешается в пользу наиболее вероятного варианта).
Также следует принимать во внимание отличия 1.2.1 цифровых двойников от других компьютерных моделей.
3.3.1. Машинное обучение представляет собой методику компьютерного моделирования, направленную на повышение точности компьютерной модели на основе сопоставления результатов работы модели с фактическими данными [III.6, III.7, III.8].
Машинное обучение подразумевает применение компьютерной модели к исходным данным, для которых известен фактический результат. Такой постановке задачи точно соответствует мониторинг зданий и сооружений [III.9, III.10, III.11, III.12]:
а) имеется реальное сооружение, и его компьютерная модель;
б) имеются реальные исходные данные (фактические нагрузки и воздействия, зарегистрированные системой мониторинга, например, уровень воды в водохранилище и температура воздуха);
в) имеются реальные показатели напряженно-деформированного состояния сооружения (например, осадки в цементационной галерее);
г) необходимо повысить точность модели, а именно, чтобы при загрузке реальных исходных данных модель более точно вычисляла показатели напряженно-деформированного состояния;
д) повышение точности достигается путем корректировки некоторых параметров конечно-элементной модели.
Параметры конечно-элементной модели сооружения имеют строгий физический смысл и ясные пределы возможных значений, но при этом действительные значения многих параметров известны не точно 1.2.1 (модуль деформации, противодавление на подошву плотины, коэффициент фильтрации и т.п.).
Поэтому разрабатывается инженерная гипотеза, определяющая, какие параметры конечно-элементной модели могут быть уточнены, и в каких пределах 3.3.2 возможно их варьирование.
При таком подходе в ходе машинного обучения первоначальные значения выбранных параметров заменяются на новые, которые отражают фактические свойства сооружения, наблюдаемые в ходе мониторинга. Таким образом, происходит калибровка конечно-элементной модели, в результате которой калибруемые параметры принимают свои эффективные значения 1.2.1, а результаты моделирования совпадают с данными мониторинга.
Наиболее часто калибруемыми параметрами являются модули деформации грунтов, а калибровочными данными – осадки сооружения. Таким образом, для одних и тех же контрольных точек сооружения сопоставляются результаты расчета осадок с результатами измерения осадок датчиками автоматизированного нивелирования.
Для трех калибруемых параметров гипотеза калибровки будет выглядеть следующим образом:
Е1 = [e1min … e1mean … e1max],
E2 = [e2min … e2mean … e2max],
E3 = [e3min … e3mean … e3max],
где Ex – неизвестные модули деформации;
exm – значения модулей деформации из интервала варьирования.
Подбор комбинации параметров e1, e2, e3, при котором будут совпадать расчетные и натурные данные, чрезвычайно ресурсоемок. Если рассмотреть по 5 вариантов каждого параметра, необходимо выполнить 53 = 125 расчетов конечно-элементной модели, при 10 вариантах необходимо 103 = 1000 расчетов.
Для ускорения процесса калибровки используется математическая теория планирования эксперимента (ТПЭ) [III.13, III.14, III.15, III.16]. Вместо перебора всего множества комбинаций e1, e2, e3 выбираются только комбинации, достаточные для построения функции отклика, которая связывает варьируемые параметры с результатом расчета:
F(e1, e2, e3) = R,
где F(e1, e2, e3) – функция отклика, обычно в форме квадратичного полинома;
R – результат расчета, выражающий невязку расчетных и натурных осадок.
Необходимое количество комбинаций варьируемых параметров для построения функции отклика определяется планом эксперимента.
|
Число |
Количество комбинаций параметров |
||
|
План |
План |
Всего |
|
|
2 |
— |
9 |
9 |
|
3 |
13 |
15 |
27 |
|
4 |
25 |
25 |
81 |
|
5 |
41 |
43 |
243 |
|
6 |
61 |
77 |
729 |
|
7 |
85 |
143 |
2187 |
Далее методами математического анализа функции отклика находится искомое сочетание, при котором будут совпадать расчетные и натурные данные:
(E1, E2, E3) = arg min F(e1, e2, e3).
Найденные E1, E2, E3 подставляются в конечно-элементную модель и проводится ее верификация, т.е. работа модели проверяется в широком диапазоне нагрузок и воздействий.
Верифицированная модель интегрируется в автоматизированную систему мониторинга путем настройки программного интерфейса для автоматизированного обмена данными:
— от системы мониторинга цифровой двойник получает информацию о нагрузках и воздействиях;
— в систему мониторинга цифровой двойник передает параметры прогнозного коридора осадок для каждого датчика автоматизированного нивелирования.
Далее проводится валидация модели, т.е. ее проверка в ходе опытного периода эксплуатации, после которого цифровой двойник принимается в постоянную эксплуатацию.
3.3.2. Согласно нормативным документам, допустимый коэффициент вариации физико-механических характеристик составляет:
— для бетона 16% [ГОСТ 18105-2018 Приложение А];
— для грунтов 30% [СП 446.1325800.2019, п. 3.5].
По умолчанию интервалы варьирования принимаются в соответствии с максимально допустимым коэффициентом вариации. Однако, анализ результатов инженерно-геологических изысканий, материалов строительного контроля и другой документации может позволить уменьшить интервалы варьирования. Например, для бетонов коэффициент вариации определяется при текущем контроле прочности бетона при возведении сооружения, поэтому при наличии протоколов испытаний он может быть принят по ним.
3.3.3. Для калибровки цифрового двойника по данным мониторинга наиболее подходят результаты натурных измерений, которые:
— автоматизированы, т.е. снятие показаний осуществляется дистанционно и непрерывно с установленной цикличностью, без постоянного участия человека;
— охватывают все сооружение, т.е. имеется достаточное количество точек снятия показаний;
— репрезентативны, т.е. отражают особенности напряженно-деформированного состояния, наиболее важные для мониторинга ГТС.
В ходе компьютерного расчета методом конечных элементов 1.1.1 могут быть определены любые параметры напряженно-деформированного состояния, которые измеряются в натуре.
Однако, калибровка затруднена тем, что степень сходимости результатов натурных измерений с результатами моделирования зависит от вида измерений.
|
Измеряемый параметр |
Способ измерений |
Количество точек наблюдения* |
Возможность автоматизации** |
|
Осадки*** |
Оптическое нивелирование |
++ |
± |
|
Автоматизированное гидростатическое нивелирование |
+++ |
+ |
|
|
Плановые перемещения |
Прямые и обратные отвесы |
+ |
± |
|
Раскрытие швов и подвижки по ним |
Щелемеры |
+ |
± |
|
Относительные перемещения на базе |
Экстензометры, деформометры |
+ |
+ |
|
Относительные деформации и напряжения в бетоне |
Тензометры |
+++ |
+ |
|
Усилия в арматуре |
Арматурные деформометры |
++ |
+ |
* количество обозначено условно
** под автоматизированными наблюдениями понимаются телеметрическое (удаленное) снятие показаний приборов в автоматизированном режиме без постоянного участия человека
*** рекомендуется переход к автоматизированному гидростатическому нивелированию, что решает задачу качественного повышения цикличности наблюдений (от ежеквартальной к ежеминутной) и позволяет увеличить количество точек наблюдения
Конечно-элементная модель отражает работу сооружения в целом и оперирует эффективными характеристиками материалов 1.2.1 и эффективными параметрами напряженно-деформированного состояния, которые справедливы для моделирования сооружения в целом. Локальные искажения напряженно-деформированного состояния в модели не воспроизводятся, хотя эти искажения могут быть значительными. Например, коэффициент концентрации напряжений вокруг круглого отверстия в плите достигает 3,0.
С одной стороны, абсолютные перемещения (осадки, плановые перемещения) и относительные перемещения на большой базе (экстензометры, деформометры) характеризуют работу сооружения в целом. В этом случае расчетные и измеренные перемещения хорошо поддаются сопоставительному анализу и позволяют эффективно калибровать модель.
С другой стороны, относительные деформации и напряжения в бетоне характеризуют работу сооружения непосредственно в точке измерения, а точнее – на базе замера. На практике преобладают тензометры с базой 0,2–0,6 м. Результаты этих измерений в силу локальных особенностей и масштабного эффекта 1.2.1 значительно и разнонаправлено отличаются от эффективных параметров расчетной схемы.
Причина этого в проявлении таких локальных факторов, как качество вибрирования бетона, неравномерность распределения крупного заполнителя, температурно-усадочные трещины, ориентация арматурных стержней, местоположение рабочих швов бетонирования, последствия влияния корпуса прибора как инородного тела при уплотнении бетона, влияние корпуса прибора как концентратора напряжений и т.п.
В результате, для относительных деформаций и напряжений в бетоне расчетные и измеренные значения, как правило, мало поддаются сопоставлению. Следовательно, они мало применимы для калибровки модели. В ходе мониторинга эти результаты обычно используются не для количественного, а для качественного анализа путем отслеживания трендов (увеличение или уменьшение измеряемой величины).
Из вышеприведенной таблицы следует, что наиболее распространены и автоматизированы измерения относительных деформаций и напряжений в бетоне (а также усилий в арматуре), которые мало поддаются использованию для калибровки.
Наблюдения, более подходящие для калибровки, либо имеют недостаточную цикличность (ориентировочно один раз в три месяца для оптического нивелирования), либо не охватывают все сооружение (прямые и обратные отвесы), либо недостаточно репрезентативны (щелемеры).
Таким образом, на современном этапе основным видом натурных измерений, подходящим для калибровки цифровых двойников, является измерение осадок посредством датчиков автоматизированного нивелирования, которые имеют высокую цикличность, охватывают все сооружение и высоко репрезентативны для ГТС.
III.1) ↑ Urbanski A (2015) Numerical Modeling of Thermal, Filtration and Mechanical Phenomena in a Selected Section of a Gravity Dam. Numerics in Geotechnics and Structures: 93-108. (Download PDF)
III.2) ↑ Commend S, Kivell S, Obrzud R, Podleś K, Truty A and Zimmermann Th (2018) Computational Geomechanics. Getting Started with ZSoil.PC. (Download PDF)
III.3) ↑ Obrzud R, Truty A (2014) The Hardening Soil Model – a Practical Guidebook. ZSoil.PC Report. (Download PDF)
III.4) ↑ Truty A, Zimmermann Th. (2014) Hoek-Brown Model for Rocks. ZSoil.PC Report. (Download PDF)
III.5) ↑ Truty A (2018) Elastic-Plastic Damage Model for Concrete. ZSoil.PC Report. (Download PDF)
III.6) ↑ Burkov A (2019) The Hundred-Page Machine Learning Book. http://themlbook.com/wiki/doku.php
III.7) ↑ Hastie T, Tibshirani R, Friedman J (2008) The Elements of Statistical Learning: Data Mining, Inference, and Prediction (Download PDF)
III.8) ↑ Montgomery D C, Peck E A, Vining G G (2015) Introduction to Linear Regression Analysis. 5th Edition. https://books.google.com/books/?id=27kOCgAAQBAJ
III.9) ↑ Malekloo A, Ozer E, AlHamaydeh M and Girolami M (2021) Machine Learning and Structural Health Monitoring Overview with Emerging Technology and High-Dimensional Data Source Highlights. Structural Health Monitoring. DOI: 10.1177/14759217211036880. (Download PDF)
III.10) ↑ Singh P, Ahmad U F and Yadav S (2020) Structural Health Monitoring and Damage Detection through Machine Learning approaches. E3S Web Conf., 220, 01096. DOI: 10.1051/e3sconf/202022001096. (Download PDF)
III.11) ↑ Yuan F-G, Zargar S A, Chen Q, Wang S (2020) Machine Learning for Structural Health Monitoring: Challenges and Opportunities. Proc. SPIE, Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, 1137903. DOI: 10.1117/12.2561610. (Download PDF)
III.12) ↑ Farrar C R, Worden K (2012) Structural Health Monitoring: A Machine Learning Perspective. https://books.google.com/books/?id=2w_sp6lersUC
III.13) ↑ Montgomery D C (2013) Design and Analysis of Experiments. 8th Edition (Download PDF)
III.14) ↑ Wu J C F, Hamada M S (2011) Experiments: Planning, Analysis, and Optimization. Second Edition. https://books.google.com/books/?id=SBgehORJ7hkC
III.15) ↑ Box G E P, Hunter J S and Hunter W G (2005) Statistics for Experimenters: Design, Innovation and Discovery. Second Edition. (Download PDF)
III.16) ↑ Mason R L, Gunst R F, Hess J L (2003) Statistical Design and Analysis of Experiments: With Applications to Engineering and Science. Second Edition https://onlinelibrary.wiley.com/doi/book/10.1002/0471458503
Цифровой двойник выполняет функцию круглосуточного роботизированного эксперта 4.1, проверяющего результаты мониторинга на признаки дестабилизации технического состояния зданий и сооружений. При значительном изменении контролируемых параметров проводится автоматизированная рассылка тревожных сообщений 4.2 участникам процесса мониторинга.
Техническая поддержка 4.3 цифрового двойника выполняется квалифицированными сотрудниками и экспертами нашей компании.
4.1. Наша система автоматизированного мониторинга 4.1.1 объединяет работу цифрового двойника с работой датчиков автоматизированного нивелирования и иной контрольно-измерительной аппаратуры.
Автоматизированная система мониторинга в режиме реального времени сопоставляет перемещения и другие параметры напряженно-деформированного состояния сооружения с цифровым двойником, который определяет такие же параметры в тех же точках наблюдения при аналогичных нагрузках и воздействиях на модели сохранного сооружения (без вновь образовавшихся повреждений).
Если результаты мониторинга соответствуют цифровому двойнику, значит состояние сооружения стабильно 4.1.2. Таким образом, контроль 4.1.3 за состоянием сооружения осуществляется непрерывно без участия человека.
Цифровой двойник, будучи компьютерной моделью метода конечных элементов, обладает всеми возможностями компьютерных расчетов для решения инженерных задач мониторинга и технической эксплуатации сооружения, например, по анализу напряженно-деформированного состояния сооружения, по определению текущих коэффициентов запаса (например, по критерию прочности материала сооружения или основания).
4.2. При выявлении отклонений (нарушение прогнозного коридора, нарушение критериев безопасности) проводится рассылка сообщений по электронной почте и SMS. Сообщения настраиваются в зависимости от типа отклонения и требуемой быстроты реагирования 4.2.1 (например, инженер мониторинга получит оповещение при 60% от установленного предельного значения, а директор по эксплуатации – при 80%).
4.1.1. Автоматизированная система мониторинга – это компьютерная система, которая осуществляет мониторинг сооружения в круглосуточном режиме без постоянного участия человека, а в случае обнаружения неблагоприятных изменений технического состояния сооружения – незамедлительно информирует участников процесса мониторинга посредством электронных средств связи (электронная почта, SMS-сообщения). Автоматизированная система мониторинга выполняет следующие функции:
— дистанционно снимает показания с датчиков автоматизированного нивелирования (и другой контрольно-измерительной аппаратуры);
— управляет цифровым двойником, т.е. передает в цифровой двойник данные о текущих нагрузках и воздействиях, и получает от цифрового двойника параметры прогнозного коридора осадок для каждого датчика автоматизированного нивелирования (и для других датчиков контрольно-измерительной аппаратуры);
— анализирует показания датчиков путем сопоставления с прогнозным коридором 2.2.1 по данным цифрового двойника и с установленными критериями безопасности 2.2.1;
— формирует и рассылает по электронным средствам связи регулярные отчеты о результатах мониторинга, а при необходимости – тревожные сообщения.
Периодичность запуска цифрового двойника определяется скоростью изменения условий эксплуатации сооружения. При выходе осадок на границы проектного коридора в силу быстрого изменения условий эксплуатации (например, наполнение водохранилища при паводке) обновление цифрового двойника автоматически ускоряется.
4.1.2. Цифровой двойник контролирует неизменность технического состояния наблюдаемого объекта, т.е. подтверждает отсутствие развития деструктивных процессов, приводящих к образованию повреждений сооружения.
Этот контроль осуществляется по соответствию результатов мониторинга реального сооружения его цифровому двойнику, т.е. по соответствию измеренных параметров напряженного-деформированного состояния конечно-элементной модели сооружения. Если результаты мониторинга соответствуют цифровому двойнику, значит сооружение соответствует своей модели. Следовательно, в нем не образуются повреждения, влияющие на измеряемые параметры напряженно-деформированного состояния.
Использование цифрового двойника может быть сопряжено с погрешностями двух типов при обнаружении деструктивных процессов.
1. Погрешности ложноположительного характера, когда цифровой двойник обнаруживает изменения, отсутствующие в действительности. Такие погрешности исключаются благодаря калибровке, верификации и валидации цифрового двойника.
2. Погрешности ложноотрицательного характера, когда цифровой двойник не выявляет изменения, происходящие в действительности. В случае отличия реального сооружения от своей модели, расхождение результатов мониторинга с данными цифрового двойника будет усиливаться при изменении нагрузок и воздействий. Поэтому такие погрешности исключаются благодаря достаточно высокой цикличности обновления цифрового двойника, что позволяет сопоставлять результаты расчета с данными мониторинга при различных сочетаниях нагрузок и воздействий (как минимум, постоянно изменяется сезонное температурное воздействие).
4.1.3. Цифровой двойник следует рассматривать как концепцию мониторинга [IV.1, IV.2, IV.3, IV.4, IV.5, IV.6, IV.7], которая предполагает сопоставление результатов мониторинга реального объекта с результатом моделирования показаний датчиков автоматизированного нивелирования (и другой контрольно-измерительной аппаратуры) на «виртуальной копии» сооружения, т.е. на его конечно-элементной модели повышенной точности. Необходимая точность достигается в ходе разработки III цифрового двойника благодаря принципу реалистичного моделирования с машинным обучением по данным мониторинга, с дальнейшей верификацией и валидацией.
Суть этого сопоставления в том, что «виртуальная копия» сооружения гарантировано исправна (в ней не возникали новые трещины и т.п.), и поэтому демонстрирует «эталонную» реакцию сооружения на происходящие изменения нагрузок и воздействий.
Таким образом, цифровой двойник «запомнил» техническое состояние сооружения в момент своей разработки (свойства материалов, влияние швов, трещин и т.п.), и постоянно обновляет расчет напряженно-деформированного состояния по мере измерения реальных нагрузок и воздействий. Поэтому цифровой двойник «знает», какие осадки и другие показатели напряженно-деформированного состояния будут в каждый момент времени.
Отклонение результатов мониторинга реального сооружения от цифрового двойника означает, что реальное сооружение (или его основание) изменилось по сравнению с «виртуальная копией», что может быть следствием развития деструктивного процесса 2.1.1.
Изложенная концепция цифрового двойника допускает различные особенности реализации:
— цифровой двойник может моделировать как осадки, измеряемые датчиками автоматизированного нивелирования, так и другие параметры напряженно-деформированного состояния, наблюдаемые с помощью геодезических методов или посредством контрольно-измерительной аппаратуры любого типа 3.3.3;
— использование цифрового двойника возможно как в автоматизированном режиме, что рекомендуется и предполагает интеграцию с автоматизированной системой мониторинга 4.4, так и в ручном режиме, когда цифровой двойник включается инженером по мониторингу по мере необходимости;
— работа цифрового двойника возможна как в облаке, что требует надежного подключения к интернету, так и на локальной рабочей станции;
— вместе с цифровым двойником возможно использование как нашей автоматизированной системы мониторинга «Монитрон», так и другой системы, ранее развернутой на объекте, например, распространенной в России и СНГ автоматизированной системы диагностического контроля гидротехнических сооружений (АСДК ГТС) семейства БИНГ.
4.2.1. Автоматизированная система мониторинга анализирует показания датчиков автоматизированного нивелирования (или иной контрольно-измерительной аппаратуры) по двум критериям:
— сопоставление с критериями безопасности 2.2.2;
— сопоставление с прогнозным коридором 2.2.1 по данным цифрового двойника.
Нарушение критериев безопасности, которые установлены как границы допустимых пределов работы сооружения, указывает на угрозу аварии и требует незамедлительных действий в соответствии с заранее составленным планом.
Нарушение границ прогнозного коридора означает изменение закономерной работы сооружения, что свидетельствует об изменении его технического состояния. Это возможно при отсутствии угрозы гидротехнической аварии (именно предикативность мониторинга является преимуществом цифрового двойника, когда деструктивные процессы выявляются на начальном этапе развития, иногда, за годы до возникновения угрозы аварии).
Таким образом, нарушение прогнозного коридора возможно на любом этапе эксплуатации сооружения при любых нагрузках и воздействиях, что не позволяет заранее составить план действий на этот случай. Поэтому при нарушении прогнозного коридора необходим инженерный анализ для определения причин возникших изменений. Соответствующая работа должна быть организована незамедлительно.
4.3.1. Цифровой двойник требует периодического инженерного сопровождения, которое заключается в анализе накопленных результатов мониторинга, доработке и дополнительном машинном обучении 3.3.1 компьютерной модели с учетом нового опыта эксплуатации сооружения.
Это связано с тем, что первоначальный опыт эксплуатации, учтенный при разработке цифрового двойника, не является исчерпывающим, т.е. наблюдаются превышения ранее учтенных экстремумов нагрузок и воздействий. Это заметно для нестационарного температурного режима (сочетание температуры воздуха и продолжительности периода ее действия) в условиях ускорения глобального изменения климата [IV.8, IV.9, IV.10].
IV.1) ↑ Shen M, Wang L, Deng T (2021) Digital Twin: What It Is, Why Do It, and Research Opportunities for Operations Research. Preprint. (Download PDF)
IV.2) ↑ Sacks R, Brilakis I, Pikas E, Xie H S and Girolami M (2020). Construction with Digital Twin Information Systems. Data-Centric Engineering, 1, e14. DOI: 10.1017/dce.2020.16. (Download PDF)
IV.3) ↑ Jazzar M E, Piskernik M, Nassereddine H (2020) Digital Twin in construction: An Empirical Analysis. EG-ICE Workshop on Intelligent Computng in Engineering. (Download PDF)
IV.4) ↑ Zhao J, Seppänen O, Peltokorpi A, Badihi B, Olivieri H (2019) Real-time resource tracking for analyzing value-adding time in construction. Automation in Construction, 104, 52-65. DOI: 10.1016/j.autcon.2019.04.003. (Download PDF)
IV.5) ↑ Kritzinger W, Karner M, Traar G, Henjes J and Sihn W (2018). Digital Twin in Manufacturing: A Categorical Literature Review and Classification. IFAC PapersOnLine 51-11, 1016-1022. DOI: 10.1016/j.ifacol.2018.08.474. (Download PDF)
IV.6) ↑ Chacon R, Sanchez-Juny M, Real E, Gironella X, Puigagut J and Ledesma A (2018) Digital Twins in Civil and Environmental Engineering Classrooms. 4th International Conference on Civil Engineering Education EUCEET 2018. (Download PDF)
IV.7) ↑ Uhlemann T, Lehmann C and Steinhilper R (2017). The Digital Twin: Realizing the Cyber-Physical Production System for Industry 4.0. Procedia CIRP 61, 335-340. DOI: 10.1016/j.procir.2016.11.152. (Download PDF)
IV.8) ↑ Kuba M (2018) Impact of Climate Changes on Civil Engineering Structures. Preprint. (Download PDF)
IV.9) ↑ Steenbergen R D J M, Geurts C P W, van Bentum C A (2009) Climate change and its impact on structural safety. HERON 54 (1): 3-35. (Download PDF)
IV.10) ↑ Lenkei P (2007) Climate change and structural engineering. Periodica Polytechnica Civil Engineering, 51 (2): 47-50. DOI: 10.3311/pp.ci.2007-2.07 . (Download PDF)